Menu

NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site

Mixtures of Ideal Gas & Dalton law

How to calculate the pressure and partial pressures of a mixture of ideal gas ?

Follow us on Twitter 
Question, remark ? Contact us at powder.process@protonmail.com

Section summary
1. Mixture of ideal gas
2. Partial pressures
3. Dalton's Law

1. Mixture of ideal gas

Perfect Gas law / Avogadro Law

A mixture of ideal gas adopts the same behavior as a pure ideal gas, the equation of state of the ideal gas is thus still valid for the whole gas :

PV = nRT

With
P = absolute pressure of the gas
V = volume of the gas
n = quantity of the gas (in moles)
T = absolute temperature of the gas
R = perfect gas constant

In SI, P is in Pa abs, V is in m3, n is in moles, T is in K and R = 8.314

In US units, P is in PSI abs, V in ft3, n in lbmoles, T is in R, R = 10.73

Note that this expression can also be used with flow rates of gas.

2. Partial pressures

In a mixture, each gas mixed is participating to the global pressure proportionally to its molar quantity in the mixture. This participation is called the partial pressure of the gas in the mixture. The partial pressure can be calculated the following way :

Pi.V = ni.RT

With :

V = volume (total of the mixture) in m3
T = temperature in K
Pi = partial pressure of gas i in Pa abs
R = ideal gas constant
ni = molar quantity of gas i

It is then possible to sum the partial pressures within the gas :

Sum of partial pressures

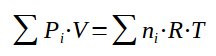
With the sum of all partial pressure being equal to the overall pressure :

Sum of partial pressure = total pressure

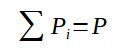
3. Dalton's law

It is possible to express the partial pressure of one of the gas constituting the mixture thanks to the molar fraction of this gas in the mixture.

Partial pressure as a function of molar ratio

With :

yi = molar ratio of gas i in the mixture

Pi = P.yi expresses the Dalton law, which means that the partial pressure of an ideal gas in a mixture is calculated by multiplying the total pressure by the molar fraction.

Note that, if only the mass ratio is known, it is possible to convert to the molar ratio thanks to the molar mass of each components.

yimol = yimass.M/Mi

With :

M = average molar mass of the mixture
Mi = molar mass of the gas i