
NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site |
Behavior of real gases
How to modify the ideal gas law to represent real gases ? Compressibility factor
Follow us on Twitter ![]()
Question, remark ? Contact us at powder.process@protonmail.com
| Section summary |
|---|
| 1. Mixture of ideal
gas |
| 2. Partial pressures |
| 3. Dalton's Law |
1. Ideal gas
Perfect Gas law / Avogadro Law
A mixture of ideal gas adopts the same behavior as a pure ideal gas, the equation of state of the ideal gas is thus still valid for the whole gas :
PV = nRT
With
P = absolute pressure of the gas
V = volume of the gas
n = quantity of the gas (in moles)
T = absolute temperature of the gas
R = perfect gas constant
2. Compressibility factor
The compressibility factor is defined as the ratio in between the volume of the real gas and the volume of the ideal gas. It is noted Z :
Z = V/Vid
With :V = volume of real
gas in m3
Vid = volume of ideal gas in m3
As the volume of ideal gas can be expressed thanks to the perfect gas law as n.R.T/P, Z can also be written the following way :
Z = (P.V) / (n.R.T)
In practice, the compressibility factor Z can be found in diagrams in the literature, typically on diagram said of Amagat. It is important to understand here that the compressibility factor allows to represent the gas, but also the liquid phase, for very low Z.
At low pressure, Z = 1, we are close to the ideal gas. When the fluid is changing phase, Z changes suddenly very strongly, from high Z to low Z in the case of a condensation.
3. Real gas law
The real gas law is a generalization of the ideal gas law thanks to the compressibility factor.
The equation of real gas law is :
P.V = Z.n.R.T
The most common relations calculated for an ideal gas (see this page), can then be adapted thanks to the compressibility factor.
3.1 Molar volume of a gas
Vm = Z*(RT/P)
3.2 Density of a gas
ρ = (P.M) / (Z.R.T)
3.3 Mass flow rate and volume flow rate
Qv = Qm*(Z.R.T) / (P.M)
3.4 Correction of volume flowrate of real gases
Qv2 = Qv1 * (Z2/Z1) * (T2/T1) * (P1/P2)
4. Law of corresponding states
4.1 Pure substances
Having a graph of Amagat to determine Z is a method but is not the simpler one. Indeed, a specific diagram is required per substance, which is not always available. Another method was then developed after scientists observed that the properties of pure substances are identical when they are at the same reduced conditions. The reduced conditions being the ratio in between the actual pressure and the critical pressure, and the actual temperature and the critical temperature. 2 substances having the same reduced conditions are in corresponding states.
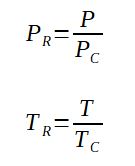
With
PR = reduced pressure
P = actual pressure
PC = critical pressure of the substance (same unit as P)
TR = reduced temperature
T = actual temperature in K
TC = critical temperature of the substance in K
As this law is actually using 2 coordinates, the law of corresponding state is said to be at 2 parameters.
Once PR and TR are determined in the conditions of the study, it is possible to use abacus to determine the compressibility factor Z. The most common graph has been developped by Reid and Sherwood in their book "The properties of Gases and Liquids". The following graph is an extension of this work at higher reduced pressure, found in Wikipedia (Daniele Pugliesi)

4.2 Mixtures
It is also possible to adapt the law of corresponding states to mixtures. To do so, a pseudo critical pressure of the mixture must be calculated by weighing the critical pressures of each components by their molecular weight. The reasoning is then the same as for the pure substances.
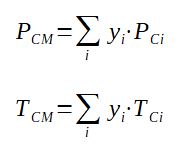
With
PCM = pseudo critical pressure of the mixture
yi = molar fraction of component i in the mixture
PCi = critical pressure of component i (same unit at PCM)
TCM = pseudo critical temperature of the mixture
TCi = critical temperature of component i (same unit at TCM)
Once calculated, Z is used in the equation of state of real fluids (see paragraph 3).
4.3 Law of corresponding states at 3 parameters
The law of corresponding state is a modelization, as a consequence, it creates some approximation and results tend to represent the reality but are not quite accurate in certain cases. In a bid to improve this, a modification of the law of corresponding states, introducing a 3rd parameter has been proposed. Different proposals were done but the theory of Pitzer, introducing the acentric factor is the most widespread.
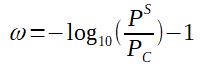
With
ω = acentric factor
PS = saturation pressure of the substance at TR = 0.7
Note that to calculate PS, one must 1st calculate what is the temperature corresponding to TR=0.7, determine T, then calculate PS(T).
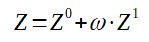
With
Z0 = compressibility factor obtained from the law of corresponding
states at 2 parameters
ω = acentric factor
Z1 = correction factor, found on abacus
Note that this method can be used but requires to use a lot of abacus. Thus other equation of states, fitting better with computer calculations were later developed.
It is possible to express the partial pressure of one of the gas constituting the mixture thanks to the molar fraction of this gas in the mixture.

With :
yi = molar ratio of gas i in the mixture
Pi = P.yi expresses the Dalton law, which means that the partial pressure of an ideal gas in a mixture is calculated by multiplying the total pressure by the molar fraction.
Note that, if only the mass ratio is known, it is possible to convert to the molar ratio thanks to the molar mass of each components.
yimol = yimass.M/Mi
With :
M = average molar mass of the mixture
Mi = molar mass of the gas i