Control valves for 2 phases flow

Calculation of Cv and mass flow through a control valve operating in 2 phases flow

Follow us on Twitter 
Question, remark ? Contact us at powder.process@protonmail.com

1. Cv and Kv definition

What is the flow coefficient Cv and Kv - calculation of flow through a valve - SI units

2. Calculation of Cv and flow through a valve - Case of 2 phases flow - metric units

What is the Cv required for a valve in 2 phases flow service ?

When a valve is operated in a bi-phasic flow at the valve inlet, the Cv required for a given mass flow rate can be estimated thanks to the following formula [Masoneilan] :

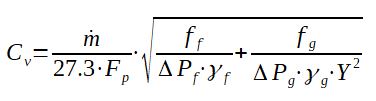
With

m=Flow rate (kg/h)
F_p = piping geometry factor (reducer correction), it is = 1 if the valve size is equal to the pipe size
C_v=valve flow coefficient (GPM)
f_f = weight fraction of liquid in 2 phases flow (-)
f_g = weight fraction of gas in 2 phases flow (-)
ΔP_f = pressure drop of liquid phase (bar)
ΔP_g = pressure drop of gas phase (bar)
γ_f =mass density of the liquid phase at inlet conditions (kg/m³)
γ_g =mass density of the gas phase at inlet conditions (kg/m³)
Y = expansion factor = 1-x/(3*F_k*x_T)

• x = pressure drop ratio = ΔP/P₁ (-)
• P₁ = upstream pressure (bar abs)
• F_k = ratio of specific heat factors = k/1.40
• k = gas specific heat ratio
• x_T = pressure drop ratio factor (this value is supplied by the constructor of the valve in product brochure). Note the value of xT can be taken as such only if the valve is used without reducers ; if used with reducers it should be corrected (not detailed in this page)

How to calculate ΔP_f and ΔPg ?

ΔP_f=F_L²*(P₁-F_F*P_v)

ΔP_g = F_k*x_T*P₁

With

ΔP_f = pressure drop of liquid phase (bar)
F_L = critical flow factor (given by the valve manufacturer)
P₁ = upstream pressure (bar abs)
F_F = liquid critical pressure factor = 0.96-0.28*(Pv/Pc)0.5
P_v = vapor pressure of liquid a flowing temperature (bar abs)
P_c = pressure at thermodynamic critical point (bar abs)
F_k = ratio of specific heat factors = k/1.40
k = gas specific heat ratio
x_T = pressure drop ratio factor