---

NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site

Valves Cv and Kv

Control valves Cv Kv flow coefficients  for valve sizing

Volumetric and mass flow of liquid and gas through valves of coefficients Cv

Follow us on Twitter 
Question, remark ? Contact us at powder.process@protonmail.com

---

1. Cv and Kv definition

2. Calculation of Cv and flow through a valve - Case of liquids - SI units
3. Calculation of Cv and flow through a valve - Case of gases - SI unitsb
4. Control valves sizing

5. Corrections of Cv for special cases

6. Calculation of flow through a valve - US units

---

1. Cv and Kv definition

What is the flow coefficient Cv and Kv - calculation of flow through a valve - SI units

The flow through a valve can be calculated thanks to the pressure drop through the valve and a coefficient Kv which represents the number of m3/h of water that goes through the valve at 15c and with a pressure drop of 1 bar.

Manufacturers may specified the coefficient Cv instead of Kv for their valve. Cv is the number of US gallons that goes through the valve at 60F and with a pressure drop of 1 psi. It is actually possible to convert Kv and Cv and have the expression in the right unit for the calculation of interest. Cv=1.156Kv

2. Calculation of Cv and flow through a valve - Case of liquids - SI units

What is the flow of liquid through a valve ?

2.1 Subcritical or critical flow ?

In order to calculate the flow of liquid through a valve thanks to the Cv, the Engineer must 1^st determine if the flow is subcritical or critical (cavitation / flashing). To do so, it is necessary to compare the pressure drop to some limit values.

• If ΔP < F_L²(ΔP_s) : the flow is subcritical
• If ΔP > F_L²(ΔP_s) : the flow is critical

With

ΔP=Pressure drop accross the valve (bar abs)
F_L = liquid pressure recovery factor = [(P₁-P₂)/(P₁-P_VC)]
P₁ = upstream pressure (bar abs)
P₂ = downstream pressure (bar abs)
P_VC = pressure at the vena contracta of the valve (bar abs)
ΔP_s = critical pressure drop = P₁ - (0.96-0.28*√(P_v/P_c))*P_v
P_v = vapor pressure of the liquid at the temperature of the flow (bar abs)
P_c = pressure at thermodynamic critical point (bar abs)

• The liquid pressure recovery factor is given by the valve manufacturer
• ΔP_s can be approximated as ΔP_s=P₁-P_v if P_v < 0.5*P₁

The relations given below are valid only for a Newtonian liquid in turbulent flow.

2.2 Subcritical flow

The volumetric flow of liquid through a valve can be calculated by Qv = Kv.√(ΔP/d) or Qv=Cv/1.156.√(ΔP/d) for subcritical flow.

With

Q_v=Flow rate (m3/h)
C_v=valve flow coefficient (GPM)
K_v=valve flow coefficient (m3/h)
ΔP=Pressure drop across the valve (bar)
d₁₅^t=density of the liquid referred to water at 15 degrees (-) - as the density of water at this temperature is 999.13 kg/m3, d₁₅^t can be approximated as ρ/1000
ρ = density of the liquid at the temperature of flow (kg/m³)

The mass flow rate through the valve can be calculated thanks to the following formula Cv=1.156*m/√(ΔP*d) ⇒ m=(Cv/1.156)*√(ΔP*d) :

With

m=Flow rate (t/h)
C_v=valve flow coefficient (GPM)
ΔP=Pressure drop accross the valve (bar)
d₁₅^t=density of the liquid referred to water at 15 degrees (-) - as the density of water at this temperature is 999.13 kg/m3, d₁₅^t can be approximated as ρ/1000
ρ = density of the liquid at the temperature of flow (kg/m³)

2.3 Critical flow

For critical flow, the following formula can be used to calculate the volumetric flow through a valve of coefficient Cv : Qv=F_L*Cv/1.156.√(ΔP_s/d)

Q_v=Flow rate (m3/h)
F_L = critical flow factor
C_v=valve flow coefficient (GPM)
ΔP_s=as defined above at paragraph 2.1
d₁₅^t=density of the liquid referred to water at 15 degrees (-) - as the density of water at this temperature is 999.13 kg/m3, d₁₅^t can be approximated as ρ/1000
ρ = density of the liquid at the temperature of flow (kg/m³)

For calculating the mass flow, the following formula can be used :

With :

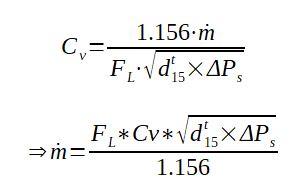
m=Flow rate (t/h)
F_L = critical flow factor
C_v=valve flow coefficient (GPM)
ΔP_s=as defined above at paragraph 2.1
d₁₅^t=density of the liquid referred to water at 15 degrees (-) - as the density of water at this temperature is 999.13 kg/m3, d₁₅^t can be approximated as ρ/1000
ρ = density of the liquid at the temperature of flow (kg/m³)

Calculation example of the flow through a valve of coefficient Cv

A control valve has a Cv of 5. The instrumentation on the line show that the pressure drop through the valve is 0.1 bar ? What is the flow through the valve. It is water at 50°c.

The density of water at 15°c is 999.13 kg/m³

The density of water at 50°c is 988.07 kg/m³

The density of water at 50°c compared to water at 15°c is : 988.07/999.13 = 0.9889

The flowrate is Qv=Cv/1.156.√(ΔP/d) = 5/1.156*√(0.5/0.9889) = 3.07 m³/h

Note : the reverse calculation can be done when knowing a flow, a pressure and wanting to calculate the Cv.

3. Calculation of Cv and flow through a valve - Case of gases - SI units

What is the flow of gases through a valve ?

The volumetric flow rate of gas through a valve can be calculated from the valve Cv thanks to the following formula :

With

Q_v=Flow rate (m3/h) at 15c and 101325 Pa abs
F_L = critical flow factor
C_v=valve flow coefficient (GPM)
P₁ = upstream pressure (bar abs)
d = gas specific gravity vs air (d_air = 1) = M/29
M = molar mass of the gas (g/mol)
T = temparature (K)
Z = compressibility factor (-)
y = (1.63/F_L)*√(ΔP/P₁)

• If y < 1.5, subcritical flow
• if y > 1.5, then y is capped at y = y_max =1.5 for critical flow

The mass flowrate through the valve can be calculated thanks to the following formula :

With

m=Flow rate (t/h)
F_L = critical flow factor
C_v=valve flow coefficient (GPM)
P₁ = upstream pressure (bar abs)
d = gas specific gravity vs air (d_air = 1) = M/29
M = molar mass of the gas (g/mol)
T = temparature (K)
Z = compressibility factor (-)
y = (1.63/F_L)*√(ΔP/P₁)

• If y < 1.5, subcritical flow
• if y > 1.5, then y is capped at y = y_max =1.5 for critical flow

4. Control valve sizing

What are the best practices to size control valves ?

In order to have a good control, the design of the control valve should be such that it represents around 1/3 of the total pressure drop of the line. The valve must also be designed to work at flows corresponding to 50 to 80 percent of the Cv of the valve.

5. Corrections of Cv for special cases

5.1 Effect of pipe reducers

The formula given above are valid when the valve diameter is equal to the pipe diameter. However, it sometimes happens that the valve is mounted in between pipe reducers which has as an effect to reduce the capacity of the valve. To account for this effect, a coefficient F_p, the piping geometry factor is calculated. The actual Cv is then :

Cv_corrected = Cv / Fp

Fp = [(Cv²*ΣK)/(0.00214*d⁴)+1]^-0.5

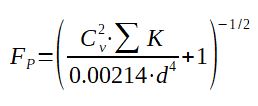
With

Cv_corrected = actual Cv of the valve in between pipe reducers
Cv = calculated Cv without pipe reducers
F_p = pipe geometry factor
d = valve diameter (mm)
ΣK = K₁ + K₂ + K_B1 - K_B2
K₁ = loss coefficient at inlet = 0.5*[1-(d/D₁)²]²
K₂ = loss coefficient at outlet = [1-(d/D₂)²]²
K_B1 = Bernoulli coefficient = 1-(d/D₁)⁴
K_B2 = Bernoulli coefficient = 1-(d/D₂)4
D₁ = inside diameter of upstream pipe (mm)
D₂ = inside diameter of downstream pipe (mm)

5.2 Effect of viscosity

According to [Baumann], the correction of the valve Cv due to viscosity is to be applied only if the fluid has a viscosity > 40 centistokes. The correction procedure requires the calculation of a correction factor F_R which will be used in a similar way as the coefficient Fp for pipe geometry.

5.3 Laminar flow

The case of laminar flow is according to Baumann calculated the same way as a correction of viscosity, which appears logic as a higher viscosity will often lead to laminar flow.

6. Calculation of flow through a valve - US units

The relations above, in US units, are expressed the following ways to calculate valves of Cv in liquid and gas applications

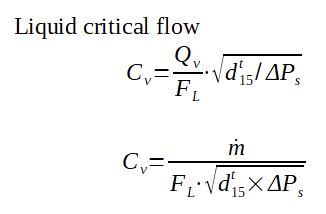
With P and ΔP in Psi abs, Q_vin GPM, C_vin GPM, m in lb/h, d is specific gravity (water = 1 at 60 F), T flowing temperature in R