Menu

Temperature profile of a wall

Calculation of the temperature profile of a wall, applications to insulation

Follow us on Twitter 
Question, remark ? Contact us at powder.process@protonmail.com

Section summary
1. Definition of heat conduction
2. Heat conduction through a wall
3. Heat conduction through a composite wall
4. Free Excel calculator for heat wall conduction

1. Temperature profile of a wall

When to calculate the temperature profile of a wall ?

It is possible to calculate the heat flux through a wall by conduction, knowing the temperatures on each surface of the wall and the thermal conductivity of the material constituting the wall. It is also possible to calculate the heat flux of a wall submitted to convection on both sides, knowing the heat transfer coefficient of each convection phenomena as well as the temperature of the gas on each side.

However those calculations are sometimes not enough, especially when having select refractants, in order to make sure that they can handle the temperature they will be submitted to, or in order to calculate a surface temperature for safety reasons or to check if condensation will happen on the wall. The following cases requiring a temperature profile calculation can therefore be highlighted :

  • Hot application : checking that refractory materials will be submitted to acceptable temperature / design the best refractory arrangement
  • Hot application : making sure the surface temperature is low enough to be safe
  • Cold application : making sure the surface temperature is high enough to be safe and / or not create icing or condensation

The calculation procedure explained in this page applies to plane wall, monomaterial or made of several layers, submitted to gas convection on both sides.

Combined conduction and convection Heat transfer

Figure 1 : Simultaneous heat transfer by convection and conduction

2. Temperature profile of a plane wall : calculation procedure

How to calculate the temperature on the surface and for each layer of composite wall ?

A typical problem is to calculate a temperature profile knowing the temperature of the gas on each side, and having an estimation of the convection coefficient on each side. The composition of the wall in terms of materials and thermal conductivity is known.

STEP 1 : make an assumption on the wall temperature on 1 side.

The calculation is actually iterative, it is necessary to make an assumption on the wall temperature on one side and check if the wall calculation is looping properly. The hypothesis on the wall temperature can be done after analyzing the heat resistances on both sides of the wall. For example, if on one side, the fluid is a liquid and on the other it is a gas, it is reasonable to think that the heat transfer coefficient on the liquid side will be very high and therefore the wall skin temperature on this side will be close to the temperature of the liquid. After estimating the temperature of one wall, the other layer temperatures are estimated and the thermal conductivity calculated - see STEP 2.

A typical dependence of the thermal conductivity on temperature is :

λ = a.T2+b.T+c

With :

λ = material thermal conductivity in W/m.°c
T = temperature of the material
a,b,c coefficients specific of the material

If there is a big temperature gradient in between both sides of the material it will be required to calculate an average thermal conductivity.

STEP 2 : estimate the temperature profile layer by layer.

With the assumption above, the temperature Tw1 is known. The other temperatures are also estimated and the thermal conductivity of each layer is calculated.

STEP 3 : calculate the overall heat transfer coefficient

The overall heat transfer coefficient for a wall, composite, exposed to convection on both sides can be expressed the following way :

1/U = R = 1/h1+e1/λ1 +ei/λi + ... +en/λn +1/h2

With :

U = overall heat transfer coefficient in W/m2.°c
R = overall heat transfer resistance in m2.°c/W
h1 = convection heat coefficient on side 1 in W/m2.°c
h2 = convection heat coefficient on side 2 in W/m2.°c
ei = wall thickness in m of the layer i
λi = material thermal conductivity in W/m.°c of the layer i

Note : it may be also required to include an additional fouling resistance to the calculation of the overall heat transfer coefficient. See this page.

STEP 4 : Calculate the heat flux

The heat flux, which is the heat transferred expressed as a function of the heat exchange area, can be calculated the following way :

Φ = Q/A = U.ΔT

With :

Φ = heat flux in W/m2
Q = heat transferred in W
U = overall heat transfer coefficient in W/m2.°c
A = heat transfer area in m2
ΔT = temperature difference of the fluids on each side of the wall in °c

The expressions can then be summarized as :

Φ = Q/A = U.(T1-T2) = (T1-T2)/R

With :

T1 = temperature of the hot fluid on one side of the wall in °c
T2 = temperature of the cold fluid on the other side of the wall in °c

STEP 5 : calculate the temperature profile by applying the equality of the flux through the different layers of the wall

The heat flux is actually constant through the different layers of the composite wall. It is then possible to express it this way :

Heat flux for a composite wall

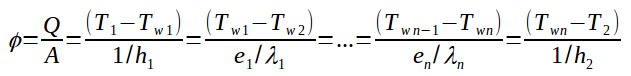
With :

Φ = heat flux in W/m2
Q = heat transferred in W
A = heat transfer area in m2
T1 = temperature of the fluid on side 1 in °c
T2 = temperature of the fluid on side 2 in °c
Tw1 = temperature on the surface of the wall on side 1 in °c
Twi = temperature at the interface in between layers i-1 and i in °c
Twn = temperature on the surface of the wall on side 2 after n layers of materials in °c
h1 = convection heat coefficient on side 1 in W/m2.°c
h2 = convection heat coefficient on side 2 in W/m2.°c
ei = wall thickness in m of the layer i
λi = material thermal conductivity in W/m.°c of the layer i

The calculation can be made directly by determining each temperature sequentially.

Calculation of the temperatures of the different layers on a composite wall

With thermal conductivity varying with the temperature

STEP 6 : compare the calculated values to the assumption

The calculated profile is compared to the assumption done in STEP 2. If those values are equal, the thermal profile has been determined and the calculation is stopped. If the difference in between assumed and calculated values is significant, the calculation is restarted at STEP 2 using calculated values determined at the previous iteration.

3. Temperature profile calculation example

The example below illustrate how to calculate the temperature profile of a wall.

The conditions are the following :

  • The wall is submitted to hot gases from the exhaust of a furnace, at 1000°c.
  • The wall is made of 3 layers of material whose conductivity is changing with the temperature.
  • The 1st layer made of material A is 100 mm, the second layer made of material B is 30 mm and the last layer made of material C is 80 mm width.
  • On the outside the wall is in contact with ambient air at 20°c
  • The heat transfer coefficient by convection on the inside of the wall is 50 kcal/h.m2.°c
  • The heat transfer coefficient by convection on the outside of the wall is 15 kcal/h.m2.°c

The material thermal conductivity can be calculated with the following data :

λ = a.T2+b.T+c in kcal/h.m.°c


 a b c
A 0 1.10-4 0.22
B 9.6.10-8 4.44.10-5 4.56.10-2
C 2.39.10-7 2.10-5 3.36.10-2

STEP 1 : Estimate the temperature on the hot wall

Looking at the data, it can be remarked that the heat transfer coefficient by convection is much higher on the hot side, we can therefor think that the wall will be hot.

STEP 2 : estimate the temperature profile layer by layer.

We assume :

Air Tw1 Tw2 Tw3 Tw4 Air
1000c 950°c 750°c 600°c 50°c 20°c

Calculate the thermal conductivity

The average thermal conductivity for the 1st layer is calculated in between 950°c and 750°c. It is equal to 0.305 kcal/h.m.°c.

Thermal conductivity of the layer 2, average in between 750 and 600°c, is 0.119 kcal/h.m.°c

Thermal conductivity of the layer 3average in between 600 and 50°c, is 0.065 kcal/h.m.°c

STEP 3 : calculate the overall heat transfer coefficient

1/U = 1/50 + 0.1/0.305 + 0.03/0.119 + 0.08/0.065 + 1/15 = 1.89 h.m2.°c/kcal

STEP 4 : Calculate the heat flux

Φ = U.(T1-T2) = 1/1.89 * (1000-20) = 518.4 kcal/h.m2

STEP 5 : calculate the temperature profile by applying the equality of the flux through the different layers of the wall

Tw1 =989.6°c

Tw2 = 819.7°c

Tw3 = 689.3°c

Tw4 = 54.6°c

T2 = 20°c

STEP 6 : compare the calculated values to the assumption

The values calculated are significantly different from those assumed. The calculation is run by using these new values as input. The calculation is done after 4 iterations, the values are expressed in °c :


Iterations 0 1 2 3 4
Tw1 950 989.631079185104 988.556156306196 988.686314957232 988.681771459257
Tw2 750 819.648770744179 804.253886632616 805.995662986264 805.97298057956
Tw3 600 689.287684310984 675.905698277456 676.489669691407 676.629169276489
Tw4 50 54.5630693829879 58.1461456460133 57.7122834758948 57.7274284691437

4. Application

This type of calculation can be applied to the insulation of a hot wall, for example in case of chimney of a furnace, to make sure the heat loss is low, the refractory materials are submitted to temperature not too high compared to their design, and that the wall is cold enough to be safe.

It is also used in the other way around, to make sure the surface temperature of a wall is hot enough in order to avoid condensation - means the wall surface temperature is higher than the dew point of the air in contact with it. This can be useful for example when calculating insulation thickness for an air conditioning duct.

5. Calculation tool for wall heat conduction

The example presented above can be found on this Excel sheet, it can be modified to fit particular cases : Temperature profile through a wall

Warning : this calculator is provided to illustrate the concepts mentioned in this webpage, it is not intended for detail design of heat transfer, insulation...etc... please consult a reputable designer for all detail design you may need.