---

NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site

Shell - Tube Heat Exchanger : pressure drop in the tubes

How to calculate the pressure drop on the tubes side of a shell-tube HX ?

Follow us on Twitter 
Question, remark ? Contact us at powder.process@protonmail.com

---

Section summary
1. Total pressure drop on the tube side
2. Pressure drop inside the tubes
3. Calculation of the pressure drop in inlet and return nozzles
4. Calculation of the pressure drop in the return cover

---

1. Total pressure drop on the tube side

The pressure drop on the tube side of a shell-tubes heat exchanger is made of several components : the pressure drop in the inlet nozzle, the pressure drop in the outlet nozzle, the pressure drop in the return cover and the pressure drop through the tubes.

ΔP_t = ΔP_i + ΔP_o + ΔP_tubes+ ΔP_c

With

ΔP_t = total pressure drop in the heat exchanger (tube side)
ΔP_i = pressure drop in the inlet nozzle
ΔP_o = pressure drop in the outlet nozzle
ΔP_tubes = pressure drop in the tubes
ΔP_c = pressure drop in the return cover

2. Pressure drop inside the tubes

How to calculate the pressure drop inside the tubes of a shell-tubes heat exchanger ?

The Bell Delaware method expresses the pressure drop inside the shell with the following formula :

ΔP_tubes = 2.f.ρ.V².L_t.Φ/d_i

With

ΔP_tubes = pressure drop in the tubes (Pa)
f = friction factor
ρ = density of the fluid (kg/m3)
V = fluid velocity in tubes (m/s)
L_t = total length of flow inside tubes (m)
d_i = inside diameter of the tubes (m)
Φ = correction factor for non isothermal flow

2.1 Friction factor calculation in tubes

The following equation allows to calculate the pressure drop :

f = 0.0014+0.125*Re^-0.32 (for Re>2100)

To be noted that the friction factor can be calculated via other correlations, more precise, accessible on Process Engineer's Tools website.

With :

Re = Reynolds number

2.2 Fluid velocity in tubes

The fluid velocity in the tubes depends on the number of tubes, the number of passes, the tube diameter and the mass flow of the fluid on the tube sides.

The number of tubes per pass can be calculated the following way :

 N_tp = N_t/n_t

The passing area of the fluid is then :

A = N_tp*(π.d_i²/4)

And the velocity is then :

V = (m/ρ)/A

With

Nt = number of tubes
n_t = number of tube passes
N_tp = Number of tubes per pass
A = passing section of the fluid (m²)
ρ = density of the fluid (kg/m3)
V = fluid velocity in tubes (m/s)
m = mass flowrate of the fluid in the tube side (kg/s)

2.3 Calculation of the total length of flow in the tubes

The total length of flow in the tubes is :

L_t = L*n_t

With

L_t = total length of flow in tubes
L = length of tubes
n_t = number of tube passes

2.4 Calculation of correction factor for non isothermal flow

The correction for non isothermal flow is due to Sieder and Tate and expressed as :

Φ = (μ/μ_w)^-0.25 in laminar flow

Φ = (μ/μ_w)^-0.14 in turbulent flow

With

μ = viscosity of the fluid at bulk temperature in Pa.s (kg/m/s)
μ_w = viscosity of the fluid at the wall temperature in Pa.s (kg/m/s)

3. Calculation of the pressure drop in inlet and return nozzles

The pressure drop in the nozzles is calculated by :

ΔP_i = 1.5*ρ_i*V_i²/2

ΔP_o = 0.5*ρ_o*V_o²/2

With :

ΔP_i = pressure drop in the inlet nozzle
ΔP_o = pressure drop in the outlet nozzle
ρ = density of the fluid (kg/m3) with indice i for inlet and o for outlet
V = fluid velocity in tubes (m/s) with indice i for inlet and o for outlet

4. Calculation of the pressure drop in the return cover

The pressure drop in the return cover depends on the fluid velocity and the number of passes. It can be calculated by :

ΔP_c = (K_e.ρ.V²)/(2.n_t)

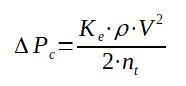
With :

ΔP_c = pressure drop in the return cover
K_e = coefficient dependent on the number of passes. 1st approximation value is 0.9 for 1 tube pass and 1.6 for multi passes tube
ρ = density of the fluid (kg/m3)
V = fluid velocity in tubes (m/s)
n_t = number of tube passes