---

NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site

Overall heat transfer coefficient

Simultaneous conduction and convection

Follow us on Twitter 
Question, remark ? Contact us at powder.process@protonmail.com

---

Section summary
1. Definition of heat conduction
2. Heat conduction through a wall
3. Heat conduction through a composite wall

---

1. Definition of the overall heat transfer coefficient

What is the overall heat transfer coefficient ?

Heat transfer is very often not only a matter of conduction, or convection, but involves both phenomena. The heat transfer can then be characterized by a heat transfer coefficient that is taking into consideration conduction and convection. Such a heat transfer coefficient is commonly called overall heat transfer coefficient.

Figure 1 : Simultaneous heat transfer by convection and conduction

For example on the figure 1, heat transfer by convection is happening on both sides of the wall, with the heat being transferred by convection on one side of the wall, it is conveyed by conduction through the wall, then transferred by convection again to the other fluid. The overall process can be translated through an overall heat transfer coefficient often noted U.

Important notice : the overall heat transfer coefficient allows to calculate the heat flux due to conduction and convection, however, in some applications, radiations must also be taken into account. This should not be forgotten and the heat flux due to radiation should be added to the one calculated for conduction and convection in order to obtain the total heat transmitted.

2. Overall heat transfer coefficient : case of a wall

How to calculate the overall heat transfer coefficient for a plane wall ?

The overall heat transfer coefficient for a wall, monomaterial, exposed to convection on both sides can be expressed the following way :

With :

U = overall heat transfer coefficient in W/m2.°c
R = overall heat transfer resistance in m2.°c/W
h₁ = convection heat coefficient on side 1 in W/m2.°c
h₂ = convection heat coefficient on side 2 in W/m2.°c
e = wall thickness in m
λ = material thermal conductivity in W/m.°c

In case the wall is made of several layers of materials with different thermal conductivities, please refer to this page detail the heat transfer coefficient for conduction.

The heat flux, which is the heat transferred expressed as a function of the heat exchange area, can be calculated the following way :

Φ = Q/A = U.ΔT

With :

Φ = heat flux in W/m2
Q = heat transferred in W
U = overall heat transfer coefficient in W/m2.°c
A = heat transfer area in m2
ΔT = temperature difference of the fluids on each side of the wall in °c

The expressions can then be summarized as :

Φ = Q/A = U.(T₁-T₂) = (T₁-T₂)/R

With :

T₁ = temperature of the hot fluid on one side of the wall in °c
T₂ = temperature of the cold fluid on the other side of the wall in °c

Fouling resistance

It may happen that the wall surface is actually not clean and a deposit of some sort is present. This deposit, called fouling, is limiting the heat transfer by adding one resistance to the overall heat transfer. The fouling resistance must be estimated and references are often found in the literature. The overall heat transfer coefficient then becomes :

1/U = 1/h₁+e/λ+1/h₂+R_F

With :

R_F = fouling resistance in m2.°c/W

3. Overall heat transfer coefficient : case of a pipe

How to calculate the overall heat transfer coefficient for a pipe ?

The same principle is applied for a cylindrical wall, and especially for a pipe, as explained above for a plane wall, to the exception that the conduction resistance is adapted to the geometry of a pipe.

For a pipe, the overall heat transfer coefficient is expressed the following way :

1/U = R = 1/h_ic+((D_o/2λ)*ln(D_o/D_i))+1/h_o

With :

U = overall heat transfer coefficient in W/m2.°c
R = overall heat transfer resistance in m2.°c/W
h_ic = convection heat coefficient on the inside of the pipe in W/m2.°c - warning, it is corrected to be referred to the external surface of the pipe h_ic = hi.D_i/D_o
h_o = convection heat coefficient on the outside in W/m2.°c
D_o = outside pipe diameter in m
D_i = inside pipe diameter in m
λ = material thermal conductivity in W/m.°c
ln = log neperian

The heat flux can then be calculated by :

Φ = Q/A = U.(T₁-T₂) = (T₁-T₂)/R

With :

T₁ = temperature of the fluid inside the pipe in °c
T₂ = temperature of the fluid on the outside of the pipe in °c

As for plane walls, fouling resistances must be added if required. Please be careful then to correct the internal fouling resistance to have it relate to the outside diameter of the pipe.

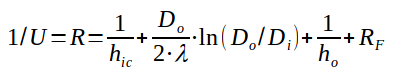
With :

R_F = fouling resistance in m2.°c/W = R_Fi.D_o/D_i + R_Fo
R_Fi = fouling resistance on the inside of the pipe in m2.°c/W
R_Fo = fouling resistance on the outside of the pipe in m2.°c/W

The expressions above are given for a monomaterial pipe, but can also be used with multimaterial, insulated pipe by referring to the conduction equations on this page.