
NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site |
Liquid Vapor Equilibrium : non ideal mixtures
What is a non ideal mixture ? How calculate the pressure and temperature at equilibrium ?
Follow us on Twitter ![]()
Question, remark ? Contact us at powder.process@protonmail.com
| Section summary |
|---|
| 1. Liquid Vapor
Equilibrium of non ideal mixtures |
| 2. Composition of
Liquid and Vapor in equilibrium |
1. Liquid Vapor Equilibrium of non ideal mixtures
Differences vs ideal mixtures
An ideal mixture can be represented through a simple model (Raoult's Law) but it is never totally true, although quite close to reality for some non polar mixtures and similar such as hydrocarbons. However, as soon as the hydrocarbons in the mixtures are less similar or if some polar compounds are introduced, the mixture is not ideal anymore : a deviation to ideality is noticed.
It is easy to notice such a deviation for binary mixtures. Indeed, when plotting the mixture equilibrium pressure, at a given temperature, as a function of the liquid molar fraction composition, the Raoult's Law is giving a linear relation. When performing an experience, if the data collected go away from this linear relation, it means that the mixture is not ideal.

2. Composition of liquid and vapor in equilibrium
2.1 Activity coefficient
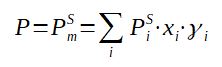
With
P = Pressure at equilibrium
PmS = Saturation pressure of the mixture
PiS = Saturation pressure of component i (note
: it is a function of the temperature)
xi = molar fraction of the component in the LIQUID phase
γi = activity coefficient of the component i in the
mixture
The simplest way to represent a deviation to ideality, i.e. a deviation from Raoult's Law, is to introduce a corrective coefficient called the activity coefficient which will increase or decrease the vapor pressure depending if the deviation is positive (higher pressure than expected) or negative (lower pressure than expected).
The activity coefficient can then be introduced in the relations associated to Raoult's Law :
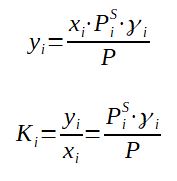
The vapor molar fraction and the equilibrium coefficient are then as well a function of the activity coefficient.
It is important to understand that, although the mathematical representation looks simple, the determination of the activity coefficient is not immediate as it depends on the temperature, the type of components but also the concentration of the different components in the mixture.
Some models are used to estimate the activity coefficients : Wilson, NRTL, UNIQUAC and UNIFAC.
2.2 Fugacity
For non ideal mixtures, the movement of particles from one phase to another is not dependent on the actual pressure, which is the case for the ideal mixtures. The actual equilibrium somehow happens as if another pressure were to be applied to the mixture. This effective pressure, which is explaining the observed equilibrium, is called the fugacity.
The fugacity can be expressed for the liquid phase and for the vapor phase. If fugacities are equal, the system is at equilibrium.
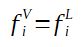
For having a mixture at equilibrium, for each component of the mixture the fugacity of the component i in the liquid phase must be equal to the fugacity of the component i in the liquid phase.
The fugacity is calculated as a function of the pressure, the molar fraction of component i in the vapor phase or liquid phase and a correction coefficient called fugacity coefficient
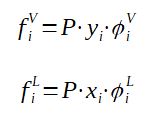
It is possible to calculate the fugacity coefficient thanks to equations of states (such as the Soave-Redlich-Kwong [SRK] equation).
Having both fugacity coefficients calculated thanks to the Soave-Redlich-Kwong equation of state then allows to calculate the equilibrium coefficient Ki. To get the following equation, it is necessary to pose fiL = fiV at equilibrium.
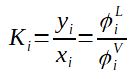
To be noted that the approach using the SRK model is working only with non polar compounds. Other methods, reintroducing the activity coefficient γ are then required for such mixtures.