NEWS : Process Engineer's Tools is moving to a new address, www.MyEngineeringTools.com, click here to discover the site

Flash Equilibrium Calculation of a mixture

How to calculate the pressure and composition of phases of a mixture of ≥ 2 components at equilibrium (flash calculation)

Follow us on Twitter
Question, remark ? Contact us at powder.process@protonmail.com

Section summary
1. Liquid Vapor Equilibrium
2. Calculation of Liquid and Vapor in equilibrium

1. Liquid Vapor Equilibrium

What needs to be calculated ?

When performing a liquid / vapor calculation, the characteristics of the infeed are available (flow rate and composition) while the characteristics of the vapor phase and liquid phase must be calculated (flow rate and composition). For solving this calculation it is also required to fix the conditions of the phases and / or pressure and / or temperature depending on what needs to be calculated.

For such a system, the following relations can be established

1.1 Material Balance

A = V + L

With

A = flowrate of infeed (mol/s, can be also kg/s if expressed in mass fraction)
V = flowrate of vapor (mol/s or kg/s)
L = flowrate of liquid (mol/s or kg/s)

1.2 Balance on each component

A.z_i = V.y_i + L.x_i

With

z_i = molar or mass fraction of component i in the infeed
y_i = molar or mass fraction of component i in the vapor
x_i = molar or mass fraction of component i in the liquid

Also

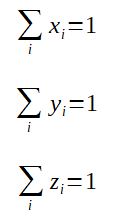
1.3 Equilibrium coefficient

Ki = y_i/x_i

y_i = K_i.x_i

With

K_i = equilibrium coefficient for component i

2. Calculation of liquid vapor equilibrium

2.1 Liquid at saturation and vessel at given pressure

In the 1^st case studied, the infeed is purely liquid at its bubble point (which means it is just at saturation, but no phase change has happened yet, the infeed is only liquid). The Engineer wants to know what is the temperature corresponding to the bubble point.

z_i = x_i (no vapor phase)

y_i = K_i.x_i (general equilibrium expression) ⇒ y_i = K_i.z_i

Σ K_i.z_i = 1

P is given

It is then necessary to have a model to calculate the equilibrium coefficient. It can be quite simple if the mixture is ideal (K_i = P_i^S / P) or more complex and require an equation of state. in any case, it is necessary to estimate the temperature to perform the calculations as K_i = f(T).

The following calculation procedure is then applied :

Estimate the temperature T
Calculate K_i = f(T)
Calculate Σ K_i.z_i
If Σ K_i.z_i = 1, T is correct and equal to the bubble temperature of the mixture
If Σ K_i.z_i ≠ 1, T needs to be recalculated by assuming a new value and going through the calculation procedure again

2.2 Vapor feed at saturation and vessel at given pressure

In the 2^nd case studied, the infeed is purely gaseous at its dew point (which means it is just at saturation, but no phase change has happened yet, the infeed is only vapor). The Engineer wants to know what is the temperature corresponding to the dew point.

z_i = y_i (no liquid phase)

y_i = K_i.x_i (general equilibrium expression) -> z_i = K_i.x_i ⇒ x_i = z_i/K_i

Σ x_i = 1

Σ z_i/K_i = 1

P is given

It is then necessary to have a model to calculate the equilibrium coefficient. It can be quite simple if the mixture is ideal (Ki = P_i^S / P) or more complex and require an equation of state. in any case, it is necessary to estimate the temperature to perform the calculations as K_i = f(T).

The following calculation procedure is then applied :

Estimate the temperature T
Calculate K_i = f(T)
Calculate Σ z_i/K_i
If Σ z_i/K_i = 1, T is correct and equal to the bubble temperature of the mixture
If Σ z_i/K_i ≠ 1, T needs to be recalculated by assuming a new value and going through the calculation procedure again

2.3 Flash equilibrium calculation

In a flash drum, the conditions of the infeed are such that, when it arrives in the flash vessel at a lower pressure, it separates immediately in 2 phases in equilibrium.

A.z_i = V.y_i + L.x_i(general mass balance)

y_i = K_i.x_i(equilibrium) -> A.z_i = V.K_i.x_i + L.x_i⇒ x_i = A.z_i / (V.K_i + L)

Σ x_i = 1 = Σ [A.z_i / (V.K_i + L)]

P is given

An iterative calculation is then required

Estimate the liquid flow L
Calculate V = A - L
Calculate K_i and Calculate x_i
If Σ x_i = 1, L is correct and the flash calculation is done
If Σ x_i≠ 1, a new value of L needs assumed and the calculation re-run

The method above works well when Ki = P_i^S/P and therefore only depends on the pressure and temperature. If it is not the case, then it is required to have another iteration loop after step 3. After calculating x_i and y_i, the coefficient K_i is recalculated. If it gives the same x_i as 1st calculated, then we can go to step 4, if not K_i is calculated again with the new composition values until it converges.