Welcome to

---

Hopper Design - Flow of Powder & Discharge

Hopper / Silo Design Calculation Method & Interactive Tool

Follow us on Twitter  
Question, remark ? Contact us at admin@powderprocess.net

---

Section summary
1. Silo / Hopper Design Calculation Methods (Jenike & Beverloo)
2. Interactive Silo Sizing Calculator (#calc-app)
3. Discharging Aids & Air Balancing
4. Engineering Best Practices & Rules of Thumb

---

What this page is about

Powder handling processes are made of many unit operations, some complex, some that can seem easier. Discharging powder is often overlooked, however, issues in this a priori simple operation can lead to huge losses.

Discharging powder must be

• Reliable
• Fast enough
• Controlled

The performance of an industrial process will be judged, among other parameters, according to its capacity to reach a nominal speed (expressed in terms of throughput, cycle time or number of batches / h). If a hopper which is supposed to deliver powder at a given rate cannot do it, be it placed at the beginning, middle, or end of the process, the whole installation "speed" will be affected.

This page will allow you to :

• Design a silo / hopper in order to ensure a good flow
• Estimate the discharge rate of a silo / hopper
• Take action in case of flow problems

Note that the way a powder is flowing depends on its properties. General powder properties, including flow properties, are listed in this page : Powder Properties.

---

1. Silo / Hopper Design Calculation methods

1.1 Why it is important

Powder has a given ability to slide and fall when it is stored in a hopper. A key variable that will have an impact on the flow of product outside of a bin is its cohesive strength.

In a bin, the powder is submitted to pressure, due to the height of powder in the bin pushing on the powder below. Due to this pressure, some solids tend to become more cohesive, forming arches or ratholes—two phenomena very detrimental to gravity discharge.

However, the stress (pressure) profile in a bulk solid silo is fundamentally different from hydrostatic liquid pressure.

Figure 1 : Stress profile in bulk solids silos (Janssen effect)

The powder is consolidated in the top cylinder section due to Janssen stress saturation. In the hopper cone, the consolidating stress decreases, minimizing the forces driving gravity flow: arching (cohesive bridging) can thus occur. Proper design finds the hopper angle and outlet diameter necessary to maintain stresses high enough to break arches and establish reliable mass flow.

Table 1 : Key Silo Design Parameters

1.2 Calculating the silo discharge diameter with the method of Jenicke

The flow of powder in a hopper is linked to 3 core shear properties:

• Internal friction angle (\(\phi_i\)): Resistance of powder particles to move relative to each other.
• Wall friction angle (\(\phi_w\)): Friction between powder particles and the internal silo wall lining.
• Compressibility & Flow Function (FF): Unconfined yield strength (\(f_c\)) developed as a function of major consolidating stress (\(\sigma_1\)).

STEP 1 - Get information on the powder
Measure the Powder Flow Function, wall friction angle, and internal friction angle using a Jenike or rotational shear tester.

STEP 2 - Calculate the hopper angle for mass flow
Determine the maximum hopper wall slope angle (\(\theta\)) to guarantee mass flow using Jenike's design charts based on wall friction (\(\phi_w\)) and internal friction (\(\phi_i\)). Apply a safety margin of \(3^\circ\) to \(5^\circ\).

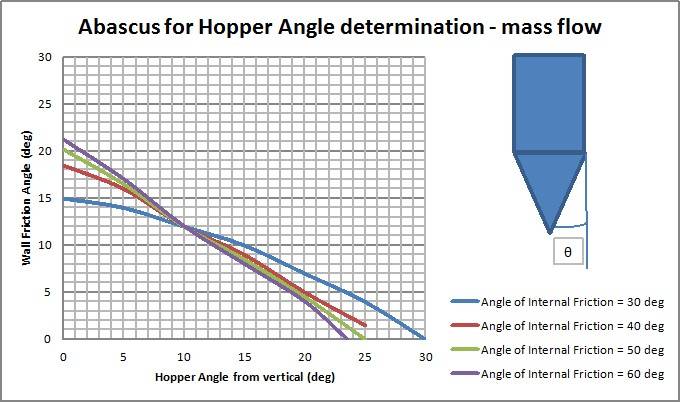
Figure 2 : Abacus for discharge hopper angle calculation [1]

STEP 3 - Calculate the flow factor (FF)
Read the Hopper Flow Factor (\(ff\)) from Jenike design abacuses using the selected hopper angle (\(\theta\)) and wall friction angle (\(\phi_w\)).

Figure 3 : Abacus for flow factor calculation [2]

STEP 4 - Calculate the critical cohesive strength (\(f_{c,\text{crit}}\))
Plot the Flow Factor line (\(\sigma_1 / ff\)) over the Powder Flow Function curve. The intersection defines the critical unconfined yield strength \(f_{c,\text{crit}}\).

Figure 4 : Flow Function and Material Flow Functions to calculate Critical Applied Stress

STEP 5 - Calculate the parameter H(\(\theta\))
Determine the dimensionless parameter \(H(\theta)\) from Jenike's abacus as a function of the hopper half-angle \(\theta\).

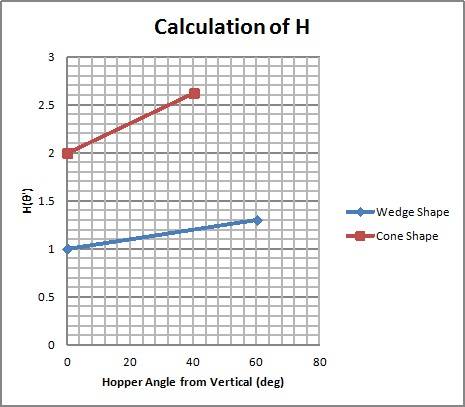
Figure 5 : Abacus for H parameter calculation (Red: axisymmetric cone, Green: planar wedge)

How to calculate the outlet diameter of a silo?

STEP 6 - Calculate the critical outlet diameter to avoid bridging (arching)
The minimum outlet dimension \(d_{\text{crit}}\) to prevent cohesive arching is calculated via Equation 1:

\[ d_{\text{crit}} = \frac{H(\theta) \cdot f_{c,\text{crit}}}{g \cdot \rho_b} \]

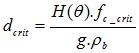
Equation 1 : Critical outlet diameter to avoid cohesive arching [2]

Where \(\rho_b\) is bulk density under consolidation, \(g = 9.81\text{ m/s}^2\), \(H(\theta)\) is the geometry factor, and \(f_{c,\text{crit}}\) is critical yield strength.

STEP 7 - Calculate the critical rathole diameter
For funnel flow silos, the minimum opening diameter to prevent stable ratholing is calculated via Equation 2:

\[ d_{\text{rathole}} = \frac{G(\phi) \cdot f_c}{g \cdot \rho_b} \]

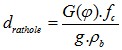
Equation 2 : Critical outlet diameter to avoid ratholing [2]

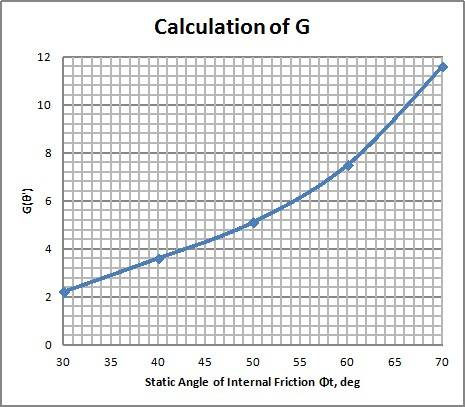
Figure 6 : Abacus for G parameter calculation

1.3 Types of bins

The primary bin flow patterns encountered in bulk materials storage are:

• Mass Flow Bin: Material is in motion at every point along the hopper walls during discharge. First-In, First-Out (FIFO) discharge. Prevents ratholing and minimizes caking.
• Funnel Flow Bin: Material flows through a central core over stagnant material near walls. First-In, Last-Out (FILO). Prone to ratholing and erratic flooding.

Figure 7 : Bin discharge patterns

1.4 Feeders used at discharge of hopper

Feeders regulate powder flow leaving the silo. Common options include screw feeders, airlock rotary valves, vibrating feeders, and butterfly valves.

Table 2 : Feeder design considerations

1.5 Calculation of the discharge rate

Coarse particles (\(d_p > 400\,\mu\text{m}\))

The Beverloo equation estimates the maximum gravity discharge rate through an orifice for coarse, free-flowing solids:

\[ W = C \cdot \rho_b \cdot \sqrt{g} \cdot (d_0 - k \cdot d_p)^{2.5} \]

Equation 3 : Beverloo equation for gravity discharge rate

• \(W\): Discharge rate (\(\text{kg/s}\))
• \(C\): Empirical discharge coefficient (\(0.55 \le C \le 0.65\), default \(0.58\))
• \(k\): Particle shape coefficient (\(1.0 \le k \le 2.0\), default \(1.6\))
• \(\rho_b\): Bulk density (\(\text{kg/m}^3\))
• \(g\): Acceleration of gravity (\(9.81\text{ m/s}^2\))
• \(d_p\): Particle diameter (\(\text{m}\))
• \(d_0\): Discharge orifice diameter (\(\text{m}\))

Johanson Equation:

\[ \dot{m} = \rho_b \cdot A \cdot \sqrt{\frac{B \cdot g}{2 \cdot (1 + m) \cdot \tan(\theta)}} \]

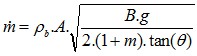
Equation 4 : Johanson equation for coarse particles

Fine particles (\(d_p < 400\,\mu\text{m}\))

For fine powders, interstitial air pressure gradients drastically reduce flow. The Carleton equation accounts for air drag resisting gravity discharge:

\[ \frac{4 V_0^2 \sin(\theta)}{B} + 15 \frac{\rho_{\text{air}}^{1/3} \mu_{\text{air}}^{2/3} V_0^{4/3}}{\rho_p d_p^{5/3}} = g \]

\[ \dot{m} = \rho_b \cdot A \cdot V_0 \]

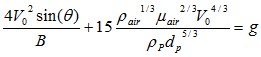
Equation 5 : Carleton equation for fine powders

---

⚠️ ENGINEERING NOTICE & EDUCATIONAL DISCLAIMER: This interactive calculator is provided exclusively for preliminary estimation and educational purposes. It is not intended for detailed design or equipment procurement without certified vendor rating. No warranty, expressed or implied, is provided, and no liability is assumed.

Interactive Silo & Hopper Discharge Calculator

Evaluate gravity discharge rates (Beverloo), minimum orifice sizing, and Jenike critical arching outlet limits in SI Metric or US Customary units.

Unit System: SI Metric (kg, m, mm, kPa) US Customary (lb, ft, in, psi)

Beverloo Gravity Flow Sizer Jenike Critical Arching Diameter

Calculation Objective: Calculate Gravity Discharge Rate (W) Calculate Required Orifice Diameter (d₀)

Target Mass Flowrate (kg/h):

Bulk Density ρb (kg/m³):

Particle Size dp (mm):

Discharge Orifice Diameter d₀ (mm):

Discharge Coeff C (0.55 - 0.65):

Shape Factor k (1.0 - 2.0):

Calculation Summary

Calculated Flow Rate (W)

-

Discharge Velocity / Intensity

-

Calculate Sizing 📋 Copy Results to Clipboard

Critical Cohesive Strength fc_crit (kPa):

Consolidated Bulk Density ρb (kg/m³):

Hopper Geometry Factor H(θ):

Engineering Safety Margin (%):

Jenike Arching Limits

Critical Arching Diameter (d_crit)

-

Recommended Design Outlet

-

Calculate Critical Outlet 📋 Copy Results to Clipboard

2. Discharging aids

A good hopper design is the primary requirement for reliable flow. However, flow promotion equipment may be necessary when handling cohesive powders, materials subject to storage caking (e.g., sugar), or inside layout-constrained vessels.

Table 3 : Discharging aids summary

---

3. Air balancing

Air balancing during hopper discharge is essential—especially for precise loss-in-weight dosing. Discharging powder displaces air: negative pressures in the discharging silo impede gravity flow, while overpressures in receiving vessels create dust clouds and valve leakage.

Figure 8 : Pressure effects during powder discharge

Properly dimensioned vent filters or pressure-equalization lines between supply and receiving bins eliminate flow restrictions caused by vacuum locking.

4. Engineering Rules of Thumb & Safety Limits (E-E-A-T)