Hopper / silo volume calculation

This page is presenting different methods to calculate the total volume of hoppers and the actual volume of bulk solids contained in hoppers, for instance for inventory purpose.

1. Volume of bulk solids contained in a hopper or a silo

When to calculate the volume occupied by solids in a silo or a hopper ?

Solids have a different behavior than liquid when they are poured in a storage vessel : they do not form a flat surface but form a heap, the heap being more or less steep depending on the nature of the solid. As a consequence, there is a strong difference in between the total volume of a hopper (what we could call the "water volume") and the volume that can actually be filled by the solid, what we would call the useful volume.

Such calculations are critical in order to design a new hopper. If one is just using the bulk density of the solids without considering the heap, there are high risks that the vessel will not be large enough. Such calculations are also very useful for existing installation when an engineer wants to check the actual volume of material in a hopper.

Note that the method presented in paragraph 3 below was published years ago, it is approximate but can be already helpful, especially in the 2nd case mentioned above, when someone wants to check the capacity of an existing hopper or know what is the amount of material in an existing hopper.

2. Total volume of a conical hopper

Calculation of the total volume of a conical hopper

Many hoppers and silos are using a conical design. It is the case studied in this page.

Such hoppers are made of :

• A conical bottom
• A cylindrical shell
• A top cover, often elliptical

Conical bottom volume calculation

The volume of a truncated cone can be calculated thanks to the following formula [aqua-calc.com]:

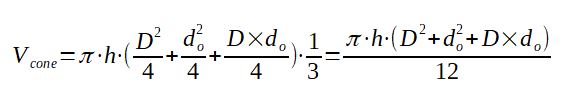
With

V_cone = volume of the conical bottom of the hopper in m³
D = inside diameter of the shell of the hopper in m
h_cone = total height of the conical discharge of the hopper in m
D_o = diameter of the outlet of the hopper in m

Cylindrical shell volume calculation

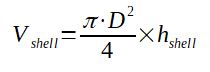
With

V_shell = volume of the cylindrical part of the hopper in m³
D = inside diameter of the shell of the hopper in m
h_shell = total height of the cylindrical part of the hopper in m

Top cover volume calculation - considering it is an elliptical cover [webcalc]

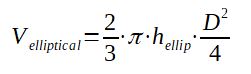
With

V_ellip = volume of the elliptical top of the hopper in m³
D = inside diameter of the shell of the hopper in m
h_ellip = height of the elliptical cover in m

Note : if the cover of the hopper is not elliptical, please adapt accordingly.

3. Actual solid inventory in a silo

How to calculate the actual volume of solids that can be stored in a silo ?

Paragraph 2 allows to calculate the total volume (or water volume) of a hopper, but what about the actual volume of bulk solids contained in this silo ?

The method [Koehler] presented allows to calculate the actual volume of material contained in the heap of product knowing :

• The diameter of the hopper
• The position of the heap (where is the material loaded in the silo)
• The angle of repose of the material

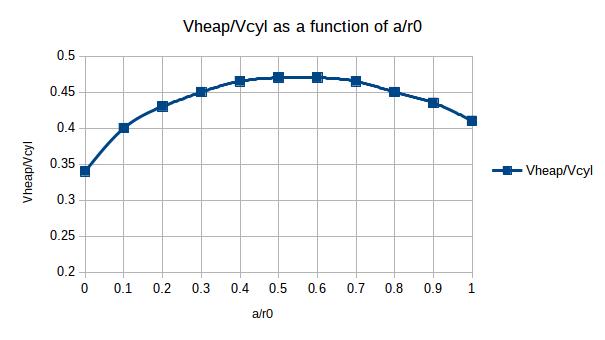
3.1 Calculate the relative position of the heap

The top of the heap is located at a distance a of the center of the silo. The silo has a diameter r₀. The ratio a/r₀ can then be calculated

3.2 Calculate the height of the heap

This calculation requires to know the angle of repose γ of the material.

The height of the heap b can the be calculated by b = (r₀+a).tan(γ)

3.3 Calculation of the volume of the heap

The volume of the heap is equal to V_heap = (V_heap / V_cyl).π.r₀².b

With V_heap / Vcyl being determined thanks to the following abacus :

3.4 Calculation of the total volume of solids in the silos

The total volume is then equal to :

V_solid = V_cone + V_cyl + V_heap

With :

V_cone = the volume of the cone filled by the solid in m3
V_shell = the volume of the cylindrical shell filled by the solid in m3, whose height is h_total - b
V_heap = the volume of the heap of solid after loading in m3

This method is applicable if the cone of the silo is entirely filled and if the method of loading is allowing the formation of the heap of product, which is typically the case when the hopper is loaded by gravity.

3.5 Rough approximation of the maximum volume of solids in a hopper

Note that at design stage, if an accurate calculation cannot be done, the following approximation can give a 1st idea of what a hopper / silo can really hold in regards to the total volume:

(max volume of product) / (total volume of hopper) = 0.8

It assumes that the formation of the heap of product will lead to a loss of 20% of the total volume of hopper, which cannot actually be filled by product. Again it is only for a very rough estimation at design stage or when troubleshooting an installation.

Source

[Koehler] Estimate the solids inventory in a silo, Frank H. Koehler, Chemical Engineering, 1982

[webcalc] http://www.webcalc.com.br/blog/tank_volume.pdf (page 7, case a = h)

[aqua-calc.com] https://www.aqua-calc.com/calculate/volume-truncated-cone